投影切断定理とX線CT
本記事はメルマガ記事A-0070. 投影切断定理とX線CTの補足です。記事本文では、投影切断定理とX線CTの関係を、
数式を使わずに説明することを試みています。
メルマガ記事もあわせてご覧ください。
- 1ラドン変換について知っておくとよいこと
- 2投影切断定理の概要
- 32Dフーリエ変換法の概要
- 4FBP法の概要
1.ラドン変換について知っておくとよいこと
ラドン変換は、CTの基礎です。
3D形状の2D透過画像をたくさん集めると、元の3D形状が一意に決まることが重要です。
これがラドン変換について知っておくべきことです。
一意に決まらなければ、2D透過画像を取っても、答えが2つ以上あることになり、CTで3D形状を再現できなくなります。
(干渉計において、干渉縞から形状が一意に決まることが重要なのと同じことです。)
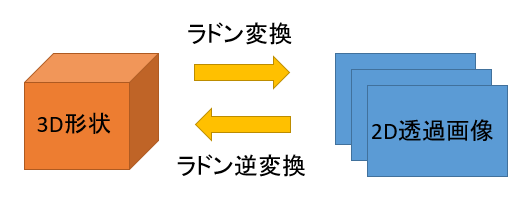
2D投影画像から元の3D形状が一意に決まります。
2.投影切断定理の概要
「投影切断定理」によって、CT再構成とフーリエ変換に関係があることが分かります。
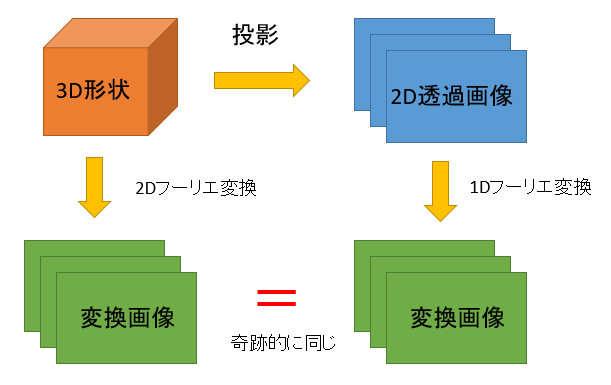
「投影」は装置がやります。
フーリエ変換やフーリエ逆変換は、コンピュータが得意な仕事です。
3.2Dフーリエ変換法の概要
投影切断定理の図をよく見ると、「2Dフーリエ変換法」というCT再構成ができることが分かります。
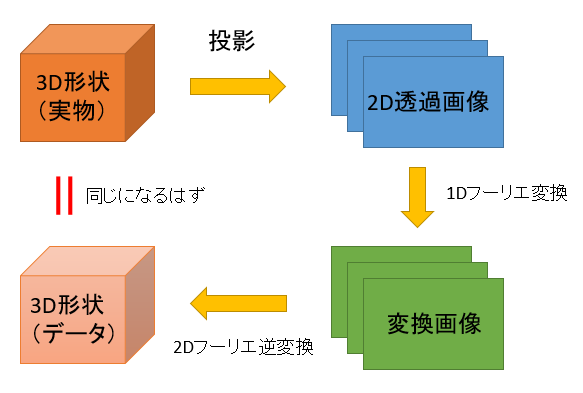
装置がやった「投影」の後、2回FFTを実行すれば、再構成できる構図。
4.FBP法の概要
「2Dフーリエ逆変換」の代わりに、
「フィルタ補正処理」→「1Dフーリエ逆変換」→「逆投影」
という演算に置き換えても、同等の答えになることが証明できます。
これを FBP法(Filtered Back-Projection ; フィルタ補正逆投影法)と呼びます。
コーンビームの場合は、開発者3人の名前から、FDK法 とも言います。
2Dフーリエ逆変換を使うよりも FBP法 の方が実用的です。
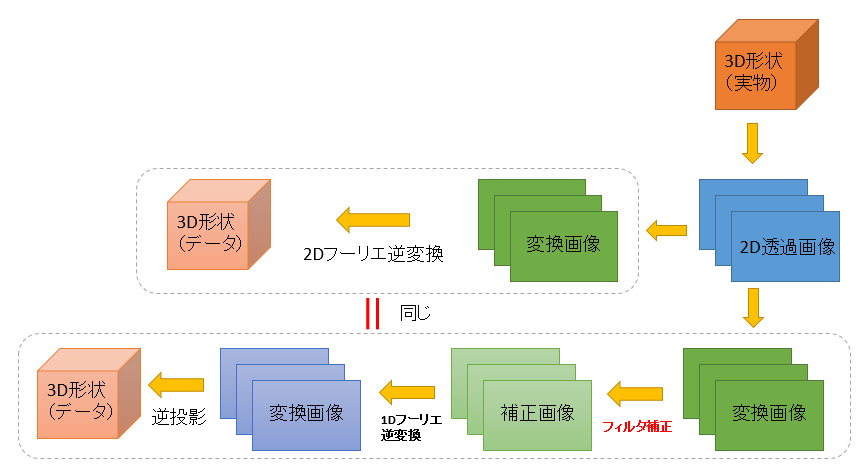
「フィルタ補正処理」→「1Dフーリエ逆変換」→「逆投影」(FBP法)
は「2Dフーリエ逆変換」と同等の演算となります。 

